DaedraMech 发表于 2023-12-19 17:02
负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力 ...

很棒，感谢

DaedraMech 发表于 2023-12-19 17:02
负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力 ...

学习了，厉害

DaedraMech 发表于 2023-12-19 17:02
负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力 ...

大佬，M2我不需要放安全系数吗？

小蜗牛zp 发表于 2023-12-19 09:03
主要是解决这个问题的同时咱能跟着学习一下，不然搞的知其然不知其所以然，以后再遇到类似的问题咋整啊， ...

这个中专的汽车专业标配，去当地找一找，减速器一般是可以自锁，估计是蜗轮蜗杆的

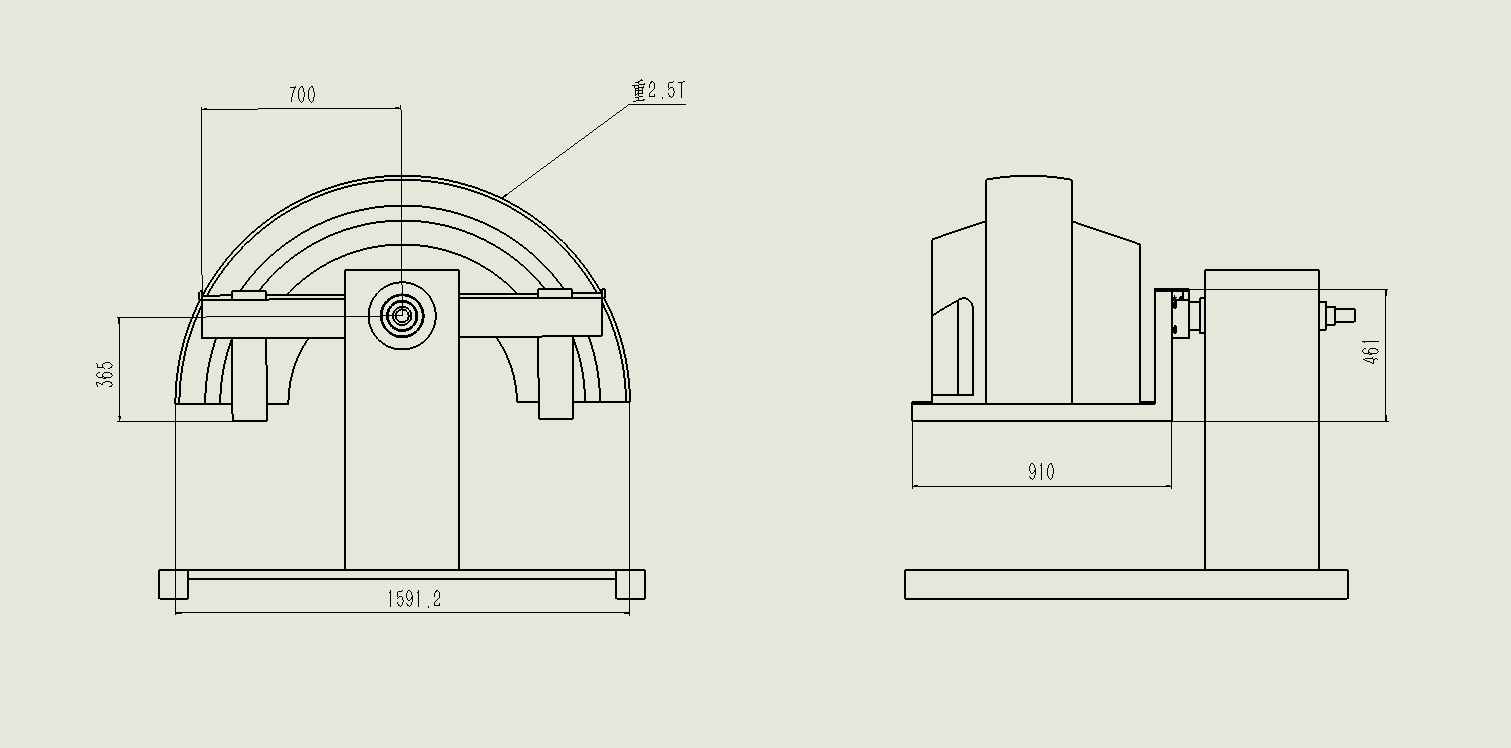
最近我也要弄这种，不过我的工件只有400kg

DaedraMech 发表于 2023-12-19 17:02
负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力 ...

很详细，非常感谢，手下我的膝盖吧，大神

DaedraMech 发表于 2023-12-19 17:02
负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力 ...

虽然看不懂，但是可以点赞！

负载需要的驱动力矩可以简单地分为三部分：一部分用来抵抗负载的惯性以达到一定转速，一部分用来克服其重力（如果有偏心），还有一部分用来克服各运动副摩擦。
接下来以你这里面2t，偏心40mm的情况为例，第一部分可以应用M=Jα。
转动惯量J可以在网上找到很多计算公式，但在SW里直接计算要快得多。此外J与转轴的位置密切相关，因此我们可以在转轴上建立坐标系来考察特定轴上的转动惯量。如图所示，我们很方便地得到了负载相对转轴的转动惯量为238.14kg·m^2（必须注意，转动惯量由积分得来，即使我使用了与你相同的质量和质心位置，只要质量的分布不同，转动惯量的结果就可能差很多，所以你不能直接拿我这里的数据套用到设备中）。

角加速度α则与你的工况相关，假设这个设备需要在2s内把负载加速到0.5转/秒，
那么α=Δω/Δt=2π·0.5/2=1.57rad/s^2。
负载如果不偏心，各运动副也十分光滑，那么就直接有M1=Jα=238.14×1.57=374Nm，通过motion仿真也得到同样的结果：

对于第二部分，由于负载偏心，我们驱动动质心升高时要克服重力做功，如图所示，这部分重力矩的变化规律比较容易得出：

即M2=mg·e·sinθ=mg·e·sinωt=2000×9.8×0.04×sinωt=784sinωt，且易知θ=90°时力矩最大，为784Nm，通过motion仿真也窥见M1、M2叠加后的力矩变化规律：

最后，摩擦力矩M3不必算出，而是可以通过机械效率（如减速机样本中的数据、各种标准件的传动效率经验表）涵盖这部分，我们假设机械效率为60%，那么合力矩M=M1+M2+M3=(M1+M2max)/0.6=(374+784)/0.6=1930Nm，通过motion仿真也可以得到三者叠加后的力矩变化规律：

而如果你最终选择了一款1：160的减速机，取个工况系数K=1.2，那最终需要的输入力矩就是Mi=1.2×M/160=19.47Nm。

LiNing_jrjub 发表于 2023-12-19 09:31
没有转速要求，没有旋转精度要求，那么就随便搞了
第一种情况不偏心，理论上让你家老母鸡用嘴啄一下也能让 ...

那这种的应该要怎么计算呢？