凸面和均质是GOMBOC (字母O上面有来年各个小点哦)的主要特性。' [% ^) g, c* O) z2 M9 D
不倒翁是非均质物体拥有GOMBOC一样行为的简单例子。
同样,因为凹面体不能通过表面圆周滚动,也很容易创造出GOMBOC均质凹面体1 Z; K5 p8 F. k: E
 ' C6 \$ z* `! [: w4 `3 [3 B
' C6 \$ z* `! [: w4 `3 [3 B
凹面GOMBOC 平面图.
只拥有唯一一个稳定平衡点的形状称作单静态体,同时拥有另外一个非稳定平衡点的称为单一单静态体。
GOMBOC是第一个凸面均质单一单静态体。& L8 a9 R( M$ Y, x c% e7 D4 U8 @
平面GOMBOC9 x/ W% J* x; S) S7 U" M
由于物体重心(G)作用,平面凸形在极坐标系中规定为函数R(a)。
' ~3 {: W# e- ~) C2 U) d/ A, h8 ^
在水平面上,所有物体都朝着重心降低的方向滚动。 R随着地面降低而变小。0 O/ ~) S F1 F: E: i; P6 \2 B
( e8 ]" B, D% E
当dR/da= 0时出现平衡点。R (d2R/da2 > 0)为最小值时,是稳定平衡点,当R((d2R/da2 < 0)为最大值时,是非稳定平衡点。R最小值后出现转而最大值,反之亦然。因此,出现稳定平衡点和非稳定平衡点次数相当。另外,下面原理也可以被证明:
* N! z2 s) L$ |, D+ r$ F; f
原理 1:
所有平面凸均质体至少有2个稳定和2个非稳定平衡点。- I! D% b. J) j8 t0 f
. I) y4 x' H0 }* ~" ?
如果物体只有一个平衡点,相应函数R(a)图就只能有一个最大值和最小值。
用直线R = R0 将物体分成两部分,函数R > R0 和R < R0 具有相等((长度p)水平投影。' s. D- L6 t7 P4 l% B+ N* l# Y1 h
) X2 O, j+ U7 a' ~( ?
相当于穿过重心G的直线相应把物体切割成薄(R < R0)和厚 (R > R0)两部分,
支撑面沿着直线。: ~: O" S; K7 k3 {8 E3 `3 P$ J: N
但是达到平衡的条件是G点不在直线上,应该在厚点的这半部分,这与之前所述G点在直线上相矛盾,由此得出原理1正确。t9 f7 V" X/ Z3 [$ \6 _
) z, i3 V+ U" { u7 ?& e
8 I' h2 S9 ?+ T$ U8 K3 u

编号为 R(
a
)的函数图(右)以及相对应的物体(左)
正如我们所证明的,不存在平面的GOMBOC型物体。这个令人惊讶的简单事实是典型数学原理的物理模拟:
四顶点定理::一条简单封闭曲线曲率至少有四个局部极值
8 [2 ?/ k, |. g" I. B/ r
有关四顶点定理有众多的概括和相关几何定理,有时这些统称为四顶点定理。
如果不存在三维GOMBOC,这个事实将成为四顶点定理家族中的又一新成员。3 G; z6 K/ r& W8 R
有关GOMBOC的基本概念% I5 i( g) |6 Q) H( _* a
/ w5 s- M Z; {9 j: w. X- \2 e
/ e" o0 B* J$ \3 N- L
类似于平面物体,三维体可以定义为重心作用下球坐标系中的函数R(j,q)# k/ z! G2 L) ]# W1 X9 K' v& d

三维体在球面坐标系中的定义
区域最小值和最大值R对应稳定平衡点和非稳定平衡点,物体在R的鞍部还有另外一个平衡点。
根据庞加莱-霍普夫(Poincaré-Hopf)理论,球体内所有同型物体,在这三种情况下,平衡值(由s, u, t,分别代表)都满足s + u - t = 2。定理1的三种假定情况:+ g4 @. ?( s/ e- o y# [) k: O
-
/ Y" Q" C$ J% R: p0 @/ I
- a)s> 1,
- b)u> 1,
- c)s + u> 2,( G0 c; K4 G+ W( a% @2 {
a) 和 b)很容易被驳倒
s = t = 1, u = 2时,s > 1为否,
8 @4 B! m8 e$ D9 g

3 K* Z1 O/ u3 p3 t: J
! p* g m! s! Z; z E& B
i > 1 时 u = t = 1, s = 2% o, |# `$ H8 t

5 H/ S L4 r7 B' J" b
+ j( y% _5 i; D# j. g1 h8 f4 M
第三种情况可能性存在于Gömböc本身:是否存在三维凸面均质s = u =1(t=0)的物体?
我们可以进一步延伸平面理论来证明这种物体存在的不可能性。* F% h8 |1 U5 N$ b- R) L; X
假设存在这种形状物体,对应函数R(j,q)就只能有一个最小值和一个最大值。0 G3 s7 T' }8 t
平面物体用R=R0分割成薄厚相同尺寸的两部分(以重心点G作为分割,两部分的空间角度相同)。
如果切割的线条是平面曲线(如:圆),则得出类似二维体的矛盾。
如果是空间曲线,则是类似网球的曲线。9 W" m1 l* _5 O* [' ]) a8 f1 h
物体分割成上下厚薄两部分,无法证明G点一定在上半部分。
由此得出平面理论并不适用于三维体。; p9 T+ h5 x3 T" e5 A2 w' s6 `
4 `" R' L3 m: \9 M4 Y

分割单一单静态体厚(黄色)薄(绿色)两部分的直线是有可能,但并不一定在一个平面上。
5 @7 [% G/ J2 q1 T. W4 j% i1 n i+ m ?1 I: L8 U
论证的失败为GOMBOC的空间形状提供了新的想法。
运用双参数闭合公式,可以分析出适当参数值得出s = u = 1物体。
受凸面体限制,构造出的物体近似于球体。
构造出的形状可以从理论推断出存在GOMBOC可能性,但是否具有单一单静态体(从视觉上可以明显看出)特性仍然是个疑问。/ P9 I4 s( |$ n& w8 g) u

应用于论证的双参数物体图形
“真正的"GOMBOC8 l/ n7 K" y# J5 e# V% w. i/ w8 \$ \
通过理论论证为什么不能找到一个具有特殊形状的物体?' v8 U1 j' k$ X' a: L# s4 H! L
是因为论证公式不好还是因为失败背后隐藏着更深层的原因?( C g* S; Y$ l L) n7 x t% U
GOMBOC具有类似球体的形状,但在罗得岛上2000多个卵石中也没能找到这种形状,这种形状如果离球体“很远"就不可能是s = i= 1。尽管寻找这种物体很困难,但是通过另一种途径却可以构造出GOMBOC的形状。以下的图示是基于网球的理念。它表面由简单图形组成(圆柱,椭圆形,锥形)和平面。显而易见,这种形状属于凸面体。通过数值积分算出其重心应稍低于原先的位置,通过这些事实,我们可以简单判断出这个形状属于单一单静态体。当然,无数的形状都可以有这些特性,而以下图形只是其中的一种。构造出来的GOMBOC样品略有不同:它由很多图块组成,这使得稳定平衡特性更健全,滚动物体的力学表现更加直观。
8 B# P; b$ n/ D4 z' T1 e- d
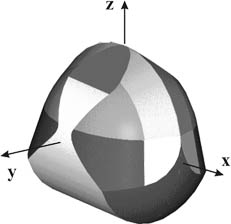
简单的图块拼接到一起构成GOMBOC 2 b" {3 ?5 S# A

在R=稳定的情况下,GOMBOC
的轮廓线能明显具有网球形状